论宇宙几何学公理体系的完备性和相容性

学半
发布于 2023-04-04 19:40
【摘要】
宇宙是一个绝对独立而完备的物质系统,运动是整个宇宙的存在形式。我们用一个真实物质(实物)的几何学形式明确定量表示一个完备宇宙的真实存在性,提出唯一的一条宇宙几何学公理:“宇宙只有一个”,那么根据该公理,能够推导出完备的宇宙物质量子的几何整数——量子数(量子是构成宇宙物质的最小成分或最基本单元),该量子数与皮亚诺公理所定义的自然数不一致。也就是说,在宇宙几何学系统中存在皮亚诺自然数自相矛盾的几何学形式。
一、几何公理体系的基本问题
1899年希尔伯特出版《几何基础》一书,对欧几里得几何学的公理体系作了系统的整理,提出了严格的几何公理体系(或称公理化体系,公理系统,公理化系统),采用了三个基本元素(点、直线、平面),五个基本关系(点在直线上、点在平面上、一点介于其他两点之间、两线段合同、两角合同),五组公理(结合公理8个、顺序公理4个、合同公理5个、平行公理1个、连续公理2个)。为明确该公理体系及各公理组间的逻辑关系,提出了公理体系的独立性、完备性和相容性这三个基本问题。并且希尔伯特证明了:只要承认实数算术系统是相容的,则这套几何公理系统是相容的、独立的和完备的。因此,欧几里得几何的相容性可归结为算术公理的相容性。
独立性:是指公理体系中的每条公理都有其存在的必要,即每条公理都不是其余公理的推论。
完备性(又称完全性或完整性):是指公理体系中有足够个数的公理,以之为依据能够证明或推导出该体系中所有的命题。
相容性(又称协调性、一致性、或自洽性):是指在公理系统中不能推导出两个互相矛盾的命题(即互为反命题的命题)。
1900年,希尔伯特在巴黎举行的国际数学家大会上作题目为“数学问题”的演讲报告,演讲中提出了23个极有学术价值的问题,俗称“23个数学问题”,对20世纪的数学发展有重要影响。其中的第2个问题就是实数算术公理系统的相容性。1988年出版的《中国大百科全书》数学卷指出,数学相容性问题尚未解决。与此有关的“物理公理的数学处理”也被列在希尔伯特23个数学问题中的第6个,公理化物理学的一般意义仍需探讨。
希尔伯特和他的学生阿克曼(Wilhelm Ackermann,1896-1962)、贝尔奈斯(Paul Bernays,1888-1977)和冯·诺伊曼在1920年至1930年间逐步地开展了所谓的希尔伯特的证明论(Beweistheorie)或元数学(meta-mathematics),这是确立任何形式系统的相容性的一个方法。希尔伯特提议,在元数学中要用一种特殊的逻辑,它应该是基本的,并且是没有异议的。它使用一种普遍承认的具体而有限的推理,很接近于直观主义的原则。不使用那些有争议的原则,诸如由矛盾去证明存在,超限归纳,以及选择公理。存在性证明必须是构造性的。因为一个形式系统可以是没有尽头的,元数学必须接纳这样一些概念和问题,它们牵连着至少是潜无穷的系统。但是,只能使用有限性的证明方法。不能涉及公式的无穷多个结构性质或无穷多个公式操作。(M.克莱因《古今数学思想》第51章第7节)
希尔伯特和他的学生阿克曼合著的《数理逻辑原理》中提到了这样一个问题:在形式系统中,真的命题是否都是可证明的?希尔伯特实际想问的是,数学中是否存在自相矛盾的真命题呢?
希尔伯特对解决这个问题是乐观的,并且断言:数学中不存在不可解的问题。
希尔伯特在《论无限》(Uberdas Unendliche)一文中说: “在欧几里得几何学和物理理论中,无矛盾性的证明是通过把它化归到算术的无矛盾性来完成的。” 现在大部分经典数学的相容性,都能够化归到自然数的算术(数论)的无矛盾性,犹如这个理论大多概括在皮亚诺公理中;或者化归到一种相当丰富的集合论足以给出皮亚诺公理。因此,自然数的算术的无矛盾性就成了注意的中心。希尔伯特和他的学派,确实证明了一些简单形式系统的无矛盾性,并且他们相信他们就将实现证明算术和集合论的无矛盾性这个目标了。
1931年哥德尔宣布完成了对不完备定理的证明,结论有两个:
第一,他证明了,任何包含自然数算术的公理系统都是不完备的,存在一些在这个系统中无法证明的命题。也就是说,要是我们能在一个数学系统中做算术的话,那么要么这个系统是自相矛盾的,要么有那么一些结论,它们是真的,我们却无法证明。
第二,他证明了,对于任意的数学系统,如果其中包含了算术系统的话,那么我们不能在这个系统内部证明它的一致性。这就是希尔伯特第二问题答案的一部分。
哥德尔第一不完备定理:任意一个包含一阶谓词逻辑 与初等数论的形式系统,都存在一个命题,它在这个系统中既不能被证明为真,也不能被证明为否。
哥德尔第二不完备定理:如果系统S含有初等数论,当S无矛盾时,它的无矛盾性不可能在S内证明。
不完备性定理要表达的意思是:如果数学是一致的,那么就不可能是完备的,反之亦然,二者是互斥的。这个发现引起了整个数学界的震动,人们认为这个定理打破了希尔伯特的美好愿望。因此大数学家外尔发出这样的感叹:“上帝是存在的,因为数学无疑是相容的;魔鬼也是存在的,因为我们不能证明这种相容性。”
尽管布劳威尔已经弄清楚了直观上明确的东西不及数学上证明了的东西多,哥德尔却证明了直观的正确会超过数学的证明。
当然,上述的论点并不排除新的证明方法的可能性,这种新方法将超出希尔伯特元数学所容许的范围。
事实上,宇宙是一个真实完备的物质系统,用一个宇宙几何学体系来描述。宇宙是所有物质的总和(如果真有上帝或“第一推动者”以及一切妖魔鬼怪或“暗物质”,那么它们都在宇宙中,统称为物质),运动是宇宙所有物质的存在形式。除了宇宙没有任何物质存在,这个概念叫做虚空(假借有形物体来虚构的空间),整个宇宙在虚空中绝对运动,虚空则绝对不动。显然,如果系统只有唯一的一条公理,就没有公理之间的矛盾。因为皮亚诺公理在宇宙系统中的真实存在性不可证明,所以,我们用真实物质(实物)的几何形式提出唯一的一条完备的公理:“宇宙只有一个”(即用一个实物的几何形式表示一个完备宇宙的真实存在性),那么根据该公理可推导出完备的宇宙物质量子数(量子是构成宇宙物质的最小成分或最基本单元),该量子数又称为“宇宙自然数”,它一定与皮亚诺公理所定义的自然数不一致。这种方法可称为“整体统一”。
再就是,1936年德国数学家根茨在使用超限归纳法的条件下证明了算术公理的相容性(一致性),该证明的前提条件在宇宙系统中是否为真亦不可证;如果为真,则一定能够被从公理“宇宙只有一个”推导出。
换言之,宇宙是一个绝对独立而完备的真实物质系统。皮亚诺公理所定义的自然数是不完备的。只有根据唯一的一条公理:“宇宙只有一个”而推导出来的宇宙物质量子数理论体系,才可能是既相容(一致或自洽)又完备(完整)的,在系统中一定存在(或包含)皮亚诺自然数自相矛盾的几何形式。宇宙几何学体系唯一的一条公理是必要且充分的。但是,为了从该公理推导出量子数,显然需要新的数学语言——物质的几何学语言,因为既有数学的形式语言所定义的实数概念及其算术命题,其存在性没有严格直观的物质几何形式作为逻辑依据来保证。正如数学史权威莫里斯·克莱因教授在他的《古今数学思想》一书中说:
“1930年以后[西方数学]的全部发展还留下来两个没有解决的大问题:去证明不加限制的经典分析与集合论的相容性,以及在严格直观的[几何]根基上去[重新]建立数学,或者去确定这种途径的限度。在这两个问题中,困难的根源都在于无穷集合和无限程序中所用到的无限(infinity)。这个概念,即使对于希腊人也已经在无理数上造成了问题,而且他们在穷竭法中躲开它。从那以后,无限这个概念一直是争论的题目,并使外尔(Weyl)说道,数学是无限的科学。”(第51章第8节)克莱因教授指出:
“欧几里得虽用图形的重合来证全等(这是根据‘公理4. 彼此重合的东西是相等的’来证明全等),但他显然对这方法是否完善无缺有点不放心。这方法有两点值得怀疑:第一,它用了运动的概念,而这是没有逻辑依据的;第二,重合法默认图形从一处移动到另一处时所有性质保持不变。你诚然证明了移过去的图形与第二个图形全等,但在原位置处的第一个图形可能不全等于第二个图形。要假定移动图形而不致改变它的性质,那就要对物理空间假定很多的条件。确实,欧几里得几何的整个目的正是为了比较不同位置的图形。欧几里得对这方法不甚放心的证据是:凡他能用其他方法来证的地方,他总不用这方法,即使是重合法能给出更简单的证明。”(第4章第3节)
“虽然直到19 世纪大半段时间以前,数学家一般都把欧几里得的著作看成是严格性方面的典范,但也有少数数学家看出了其中的严重缺点并设法纠正。第一是用了重合法。第二是有些定义含糊其词而另一些无关宏旨。开头关于点、线、面的定义没有明确数学的含义,而且(正如我们今日认识到的)不可能给出任何明确的含义,因为任何独立的数学讲解必然要用些未加定义的名词(参看第4章第3节)。至于许多定义之含糊其词,那只要回头去看看第五篇里的那些定义就足以为例了。对定义的另一不满之处是有些定义,例如第一篇中的定义17[按:定义圆的一直径所用到的圆周没有事先给出定义],应用了未加定义的概念(事先假定了一个公理)。利用今天的认识(那是理所当然的)来对欧几里得的著作进行批判研究的结果,可以发现他用了数十个他所从未提出而且无疑并未发觉的假定。”(第4章第10节)
“佩莱蒂耶在他的《欧几里得几何原本的证明》一书中,批评了欧几里得使用叠合法去证明全等方面的定理,甚至哲家学叔本华(Arthur Schopenhauer)在1844年也说,他感到很奇怪的是,数学家们攻击欧几里得的平行公设,而不去攻击重合的图形是相等的这一条公理。他论述说,重合的图形自然是相等或恒等的,因而无需什么公理;或者,重合完全是一种经验性质的事情,不属于纯直觉知识,而是属于外部感官经验。另外,这条公理预先假设图形的可移动性;但是,在空间中能够移动的是物质,因此超出了欧几里得几何的范围。十九世纪已普遍认识到:叠合法或者是建立在一些未明确说明的公理的基础上,或者必须用另一种探讨全等的方法来代替。”(第42章第1节)
不幸的是,数学界至今仍没有在叠合法上把物质自身的可移动性几何化,即仍没有在其数学公理上解决几何图形的可移动性与物质的运动形式不相容(不统一)的问题。因此,在逻辑上所有使用欧几里得几何图形叠合法去证明的全等方面的定理都不成立。于是现代数学中的数轴上的实数理论(康托尔创建的集合论及其连续统假设)以及坐标系有关的空间几何的定理和微积分理论都不成立。
实数是有理数和无理数的总称。无理数√2是从边长为单位1的正方形的对角线长不可公度这一事实得出的,但是一直都没有人给出无理数存在性的证明。19世纪戴德金利用他提出的分割理论,从对有理数集的分割给出了实数的定义。实数定义为与数轴上的点一 一对应的数,这样就构成康托的实数连续统假设。但是哥德尔认为连续统假设不可证。
关于实数点的定义和存在性,莫里斯·克莱因教授说:“亚里士多德讨论定义。他对定义的想法是符合现代精神的;他说定义只不过是给一批文字定个名。他又指出定义必须用先存在于所定义事项的某种东西来表述。因此他批评‘点是没有部分的那种东西’这一定义,认为‘那种东西’这几个字没有说出所指的究竟是什么,除非所指的可能就是‘点’[例如,除非‘点’所指的是事先给出的实物线段之‘界’],因而[‘点是没有部分的那种东西’]这个定义并不合适[合适的定义是‘点为实物线段之界’]。”而在公理化数学体系中,“定义了的东西是否存在有待于[从公理出发给出]证明,除非是少数几个第一性的东西诸如点和线,它们的存在是同[观察实物得出的]公理(第一性原理)一起事先为人们所接受的。例如我们可以定义一个正方形,而这个图形可能不存在;就是说,定义中所要求的诸属性可能无法并存。莱布尼兹(Gottfried Wilhelm Leibniz)就举出过正十面体这样一个例子;我们可以定义这样一个图形,但它并不存在。如果有人并未意识到这图形不存在就着手去证明有关这图形的定理,那他得出的结果将是胡说一气。”
值得注意的是,希尔伯特《论无限(On The Infinite)》一文中指出:“事实上,在我们的思想中,已经有一些可以作为应用逻辑推理和实现逻辑处理方法的先决条件的东西,这就是:某些逻辑以外的具体客体,这些客体是直观上作为直接经验而先于一切思维所已存在着的。要使逻辑推理可靠,那就必须对这些客体的所有部分都能完全一目了然,而它们的显示,它们的区别,它们的前后连接或左右并列,则和客体一同是所给予我们的直接直观的东西,这些东西已不可能再简化为其他东西或者需要再加以简化。”
不幸的是,希尔伯特公理体系中作为基本对象或元素的“点”已经不是直观上可直接经验的东西了,所以这种“点”以及由它集合构成的“线”以至于“面”的存在性事实上是没有逻辑依据作保证的,因而它们是单纯思辨的概念。从这些概念推出的结论也是不可靠的,即不保证都能得到经验事实的验证。
事实上,可先给出一个实物线段(图1-a₁,称为形与数统一或相结合的“1尺”)作为整个宇宙的几何抽象,再定义线上的点,点为线之界,界之间为形。线有形可分而分之不竭者(又称“量子”,古称“小之微也”或“物之精也”)仍为线。如中国古代学者用“一尺之捶[图1-a₁或图1-a₂,···亦即图1-a₆],日取其半[以直观上可直接经验的线段对折的自我量度方式定义线段中分点而取损其半,损之又损之],万世不竭[即有馀]”这种严格直观的形数结合几何学形式的理论推导,深刻入微地刻画整个宇宙内部物质耗损的排斥而量子化的过程,从而证明实物的线并不是点构成的,而是一段又一段微小的线(称为“量子”)构成的。
爱因斯坦说过:“一个理论如果要得到人们的信任,就必须建立在可以普遍推广的事实之上。……从来没有一个真正有用的和深刻的理论果真是靠单纯思辨去发现的。”莫里斯•克莱因教授说:“亚里士多德认为公理是从观察实物(物理对象)得出的,它是直接为人们所理解的一般性认识。”(《古今数学思想》第3章第10节)就是说,公理是根据物质实践的感性经验得出的。离开感性经验的认识是不可能的。实事求是,是建立科学理论的根本遵循。

二、实物的形及开始定量
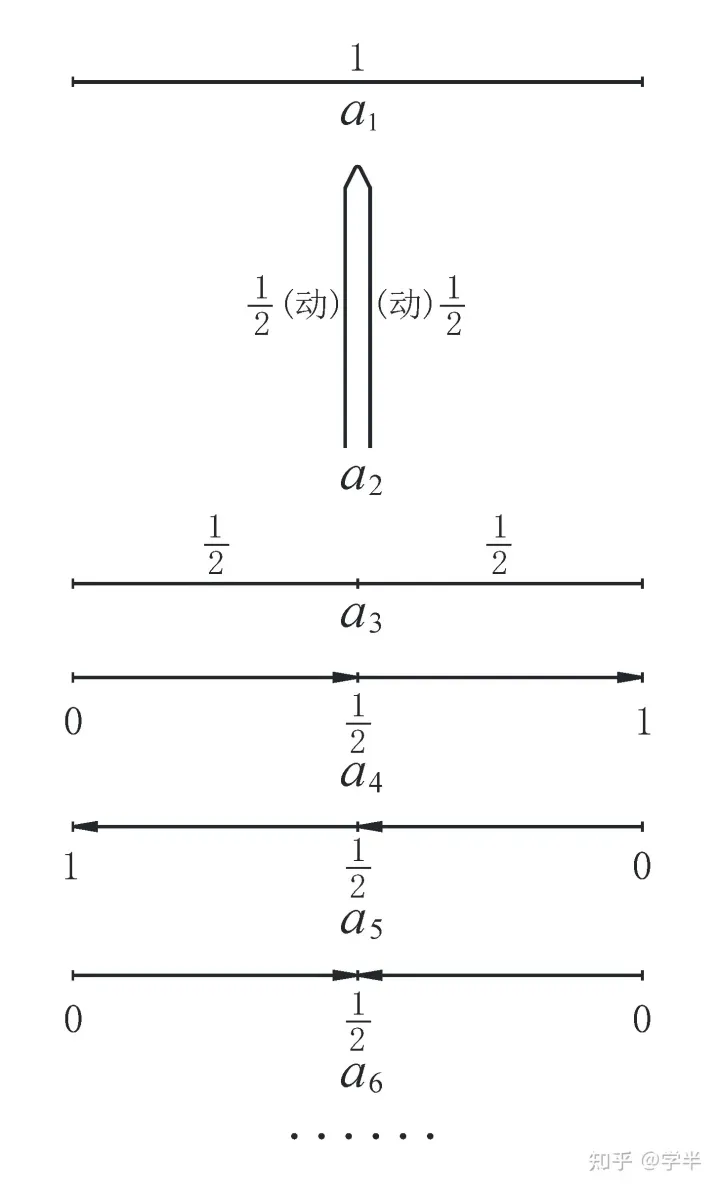
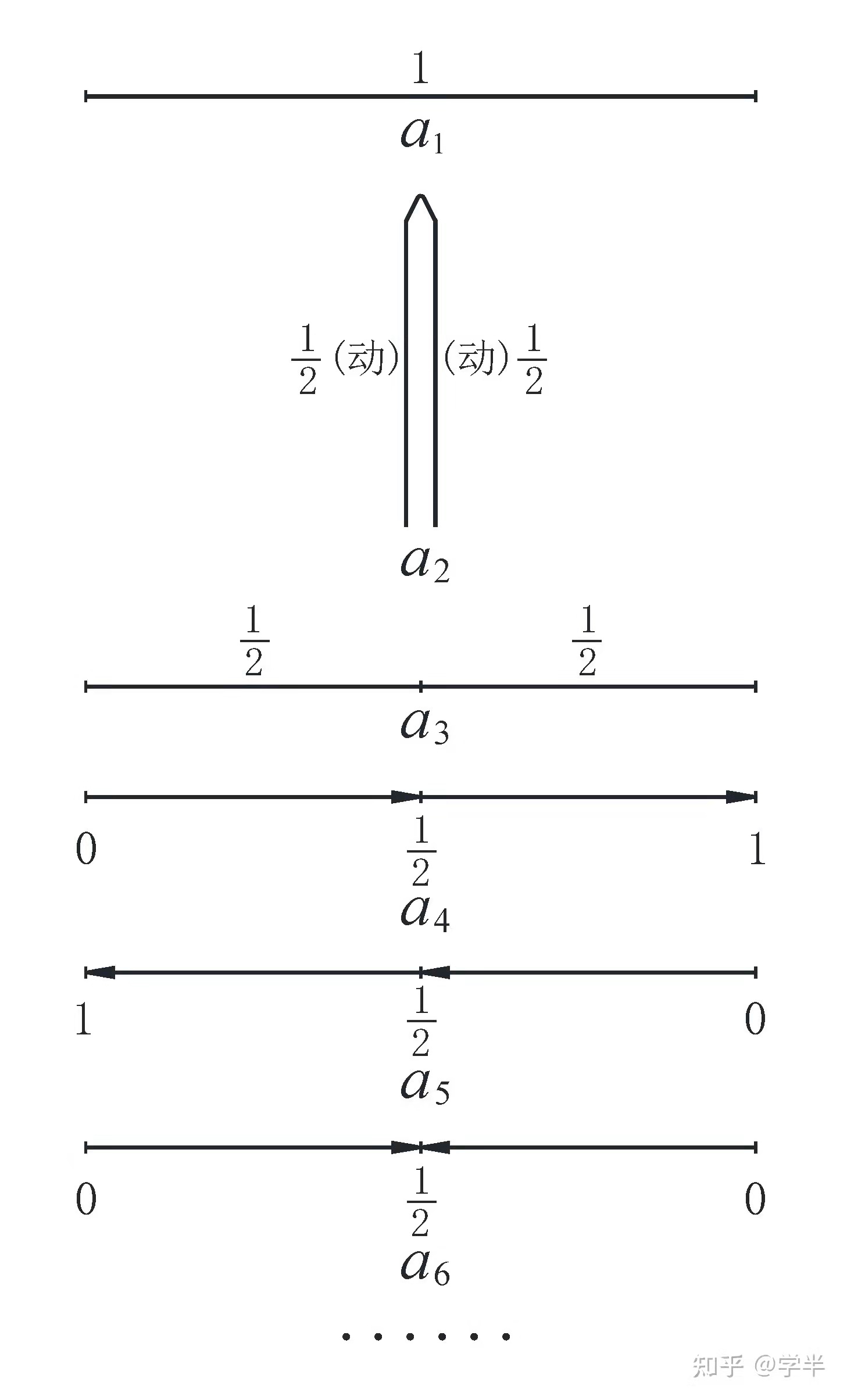
现在,我们取用一条直的草茎——线段AB(即抽象的图甲–a₁)为个别实物,接着对图甲–a₁施以一定形式的对折或自我量度(运动),则得图甲–a₂(动与不动的关系)。在图甲–a₂的基础上又对折,则得图甲–a₃(绝对动与不动的关系)。从而获得了直接经验的感性认识,即在图甲–a₃中:
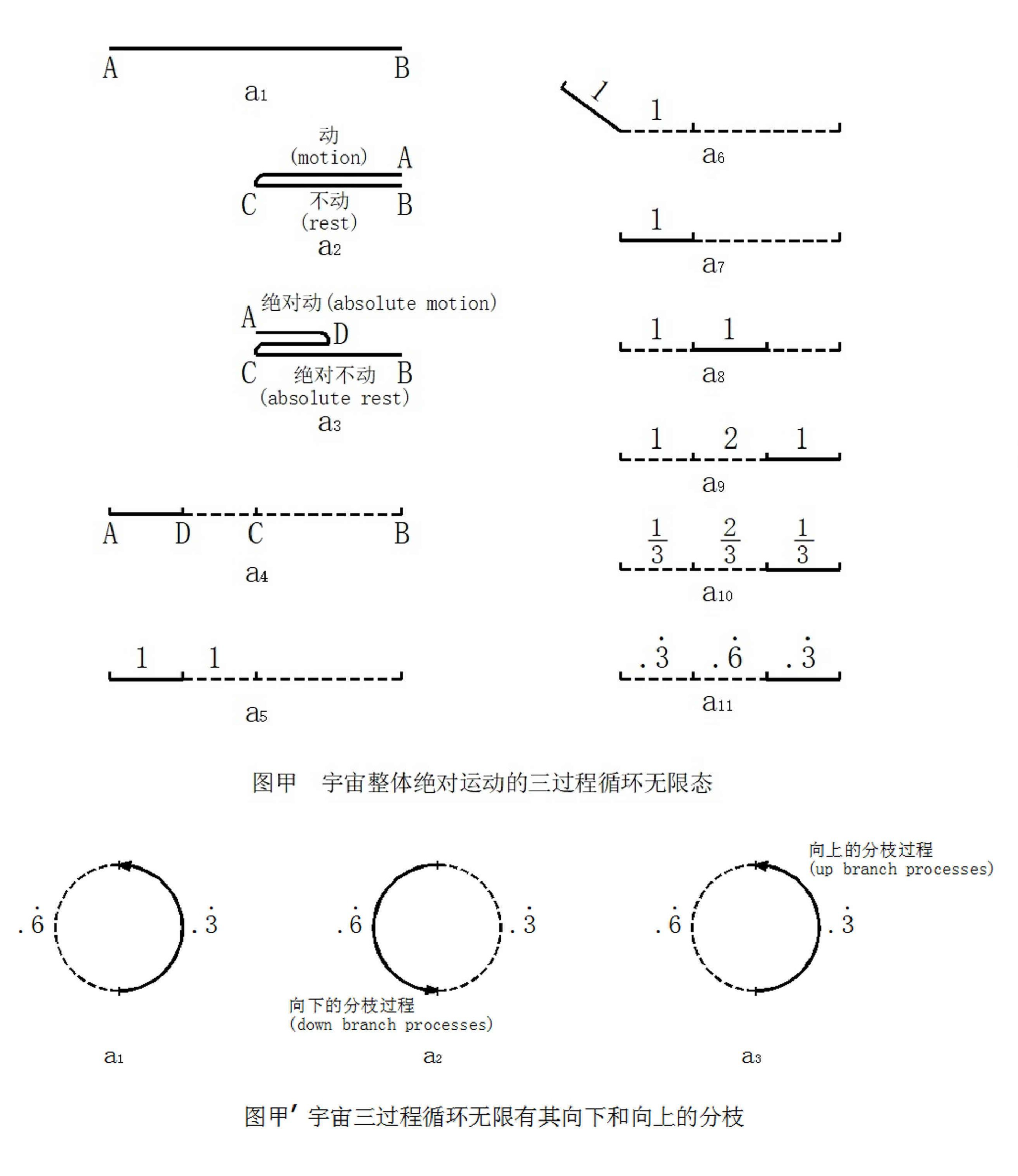
① 绝对动的物AD,是而且只能够是整个现实宇宙(又称“现实世界”)的抽象。
② 能够同整个现实世界(现实宇宙)AD重合相等的不动者DC,是而且只能够是整个现实宇宙于虚空中的容身处所。
③ 绝对不动者CB,是而且只能够是整个现实宇宙AD绝对运动的场所——虚空。
在具备了以上实践经验的感性认识后,中国人便经验方法地绳直图甲–a₃,而得图甲–a₄。在图甲–a₄中,整个现实宇宙AD显现出唯一的物质态,即中国人的实践唯物论。(毛泽东《实践论》:“离开实践的认识是不可能的。”)于是,中国人的认识论便从认识的低级阶段——感性认识的基础上,开始升华而发展到了认识的高级阶段——理性认识,从而提出了唯一的一个出发点——假设、原理或
公理:“宇宙只有一个”,
以定量地刻画整个现实宇宙(即图甲–a₅),数、形统一或相结合几何方法地探索和求解现实宇宙的各种运动,及其运动的形数结合几何学的形式规律表现。
整个宇宙发展过程中的各种运动无非是下述两大方面:一方面是整个宇宙的整体(图甲–a₅中的实者)在虚空中的运动——绝对运动(图甲–a₆,······);另一方面,就是整个宇宙(图甲–a₅中的实者,即图1–a₁)内部的各种运动——相对性运动(图1–a₂或图1–a₆,······)。
三、宇宙整体绝对运动
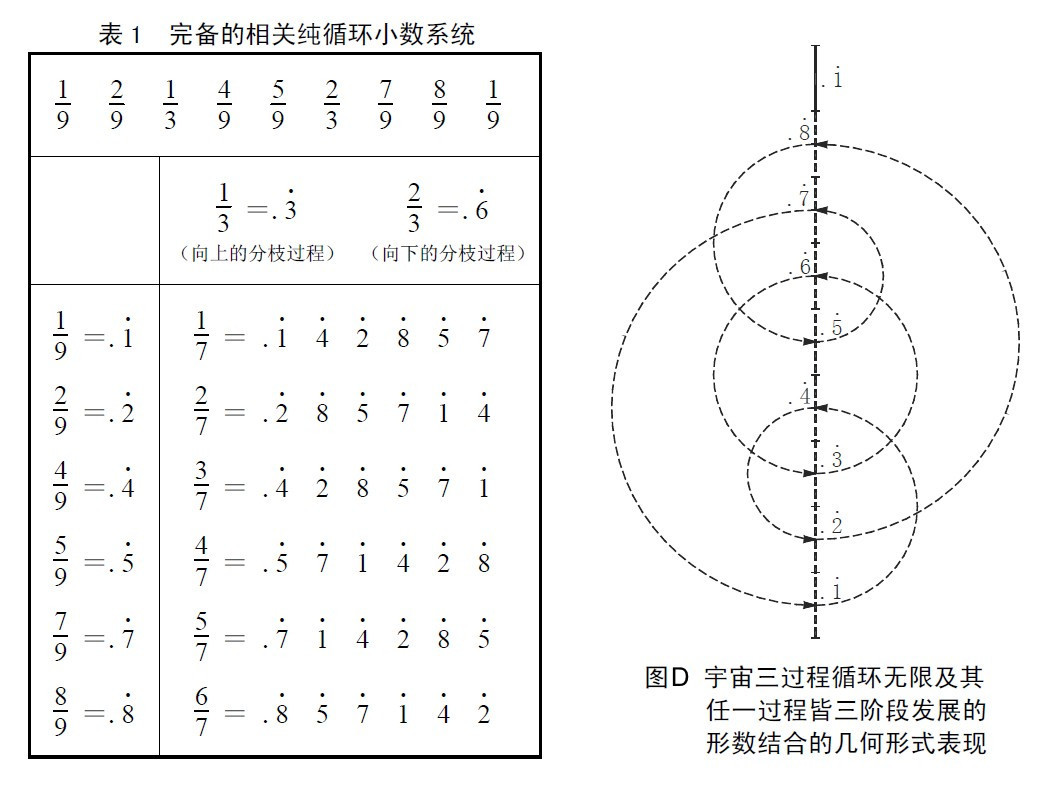
根据图甲-a₅,则得图甲-a₆及图甲-a₇;图甲-a₇为宇宙容身于虚空第一步程的状态。宇宙运动离开图甲-a₇的容身处所而运动一个步程,则得图甲-a₈;再运动一个步程,则得图甲-a₉。把图甲-a₉刻画的宇宙绝对运动的整个过程看作一个整体,则可表示为图甲-a₁₀;图甲-a₁₀亦可表示为图甲-a₁₁(其原型为图甲′-a₃)。图甲的原型是图甲′,即图甲-a₁₀中的1/3循环节的实线段叠合到1/3循环节的虚线段上作为周而复始的一步继续度量,则还原成闭环上的循环度量模型(图甲之于图甲′);其具有向下的和向上的相邻分枝过程。此即宇宙整体绝对运动具有三过程循环无限的形数结合几何学形式规律表现。同理,可进一步导出宇宙任一分枝过程皆三阶段发展的形数结合几何形式规律表现(图乙之于图丙)。
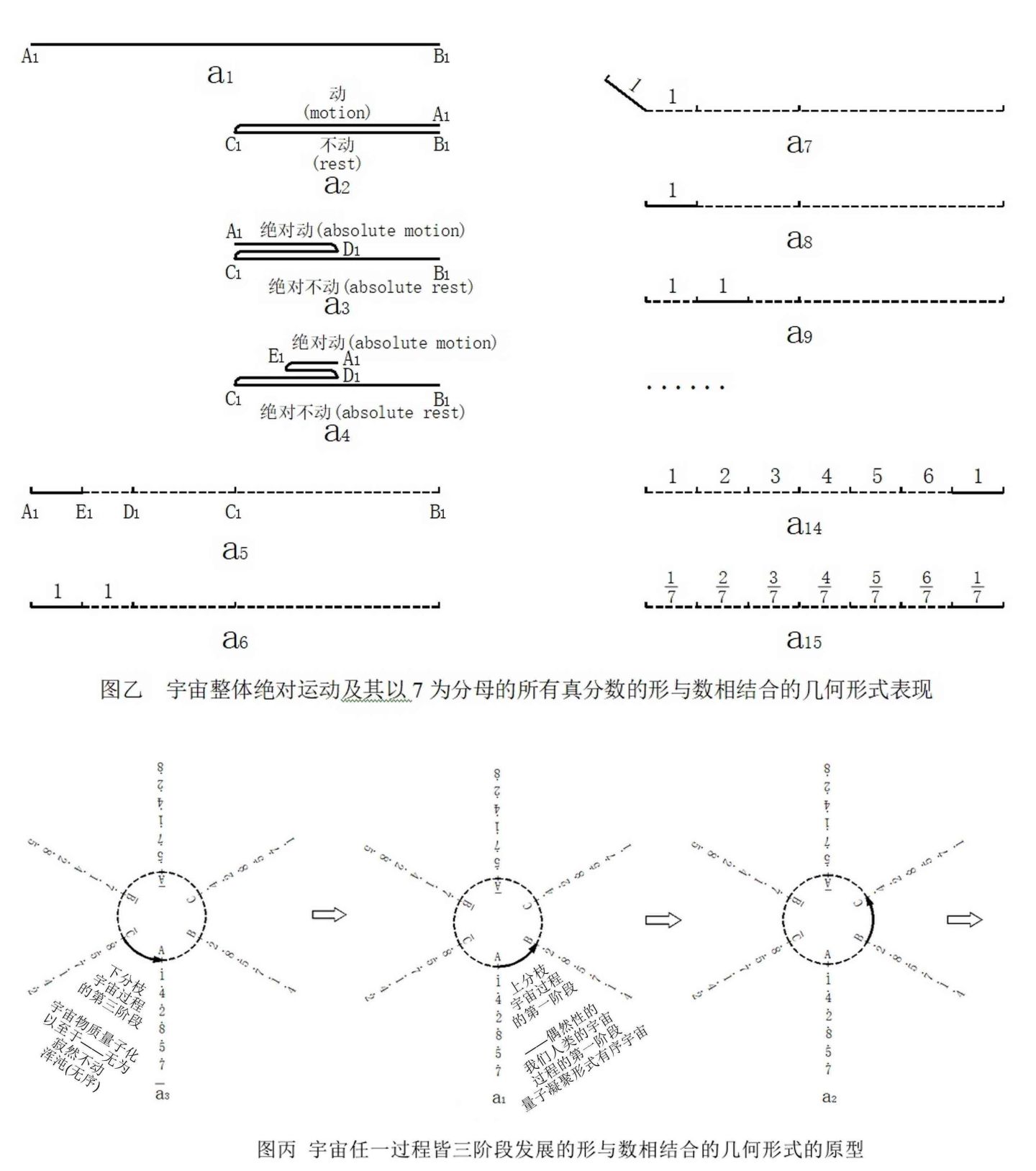

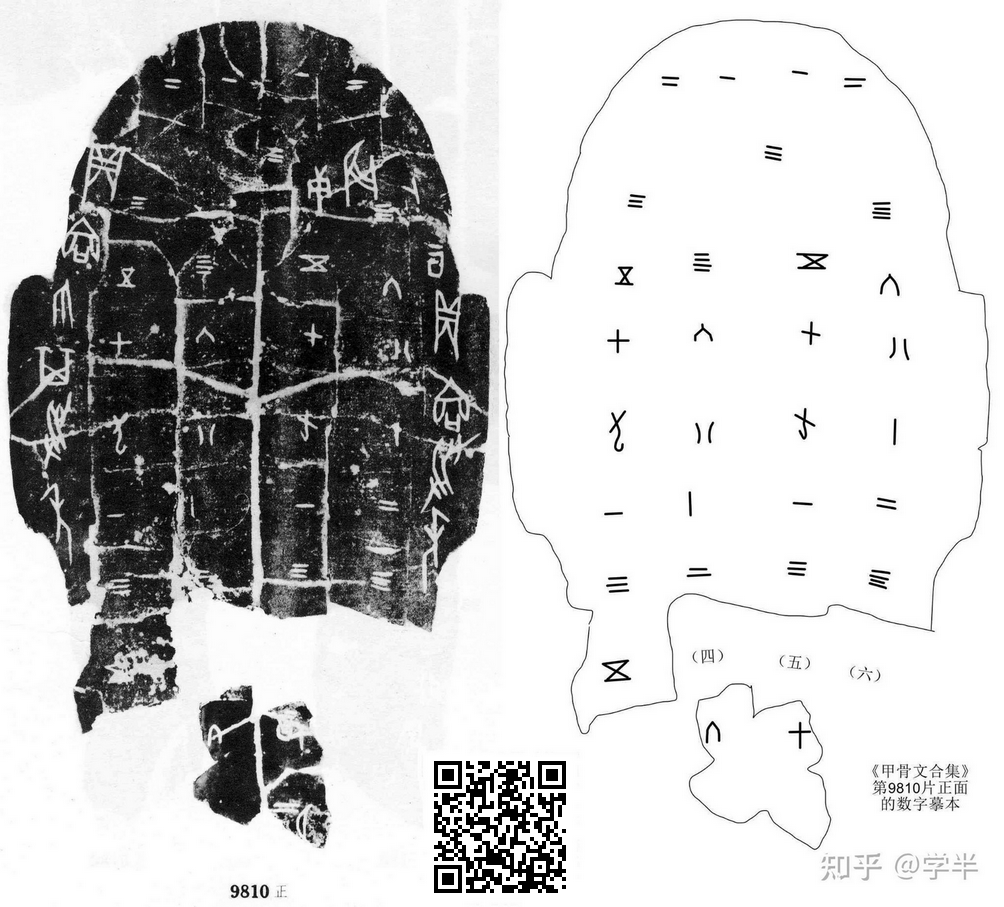
大家都知道,“昔”字的含义是过去的时间、过程(former time,past)。甲骨文“昔”字的字形由二、三条折线和“日”部构成。但几乎没有人知道,《说文解字》“日,实也”就是指“昔”字的“日”部本义是以外框强调凸显其中的度量几何单位“一”是一个实物线段“一尺之捶”,用来作为整个宇宙的几何物理抽象;即《说文解字注 · 一》记载的“一,惟初大极,道立于一”,“大极”者无非是整个宇宙的几何物理抽象。甲骨文 “昔”字中的两三条折线则表示单位“一”在表示虚空的路线上循环度量的记录:n=1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, ……(七步程循环无限态的六进位制记数法)。“昔”字的这种字形诠释了一个单位“一”循环无限进动周行而不殆的宇宙时空度量几何学模型(图乙之于图丙),这就是物质运动与时间和空间关系的理论起源。运动是物质的存在形式,时空是运动历程的刻画,空用不动的形表示,时用不动的形上的数表示,整个宇宙用绝对运动的形表示,宇宙只有一个。
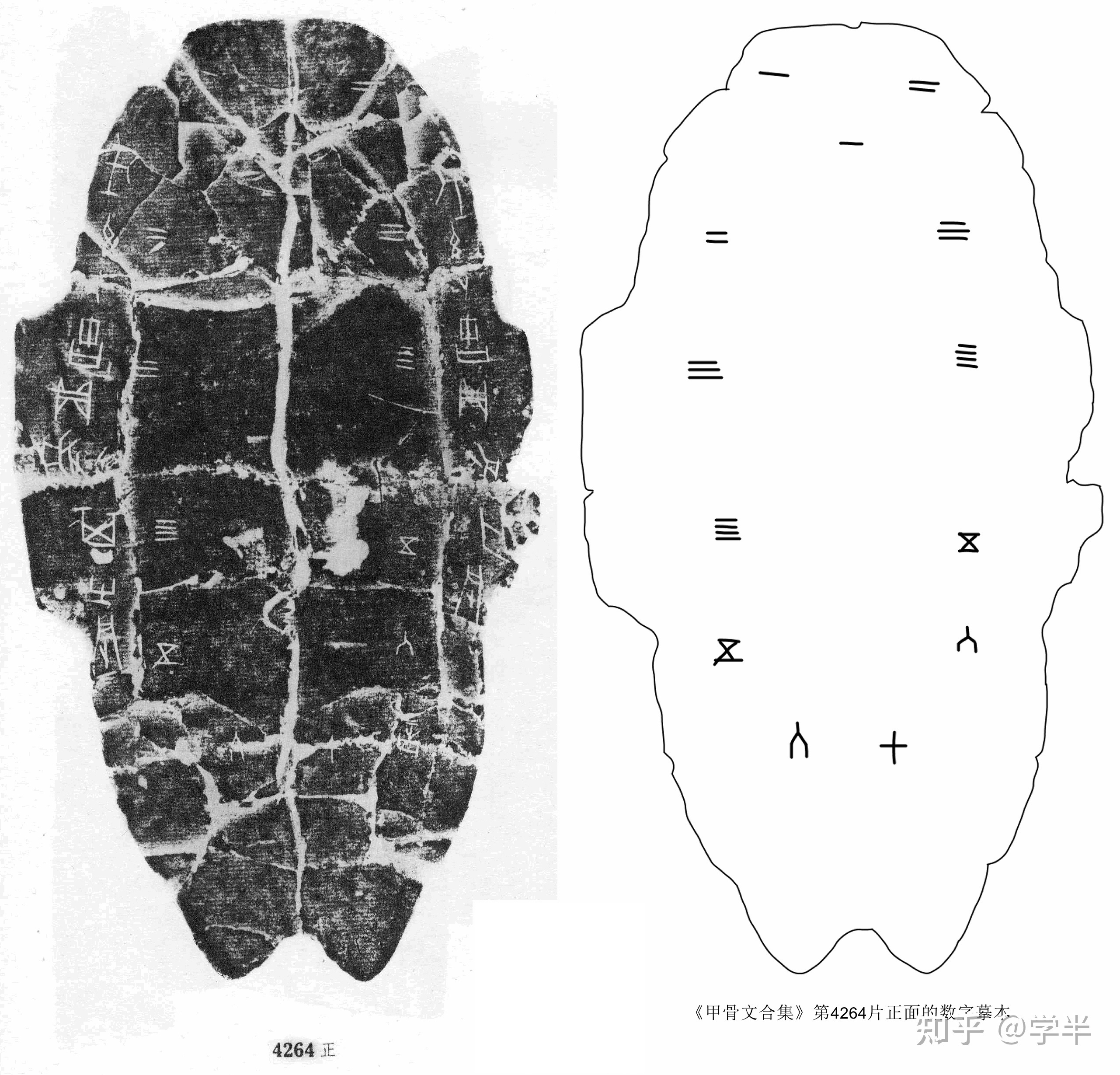
根据公理“宇宙只有一个”,将图乙-a14与图甲-a7中的宇宙之形并二合一(如图丁的右侧),即可导出综合的宇宙整体绝对运动三过程循环无限及其任一过程皆三阶段发展规律(表1之于图D)。图D中处于竖直线上方的宇宙(.1循环数实线段)每进动一步,则宇宙所经历的虚空步程数逐次加1,即可推导出十进位制循环无限记数法(见图C中的甲骨文数字),用来记录宇宙整体在虚空路线上绝对运动所经历的步程数序列n=1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ……(亦即刻画宇宙过程的时间顺序数列)。
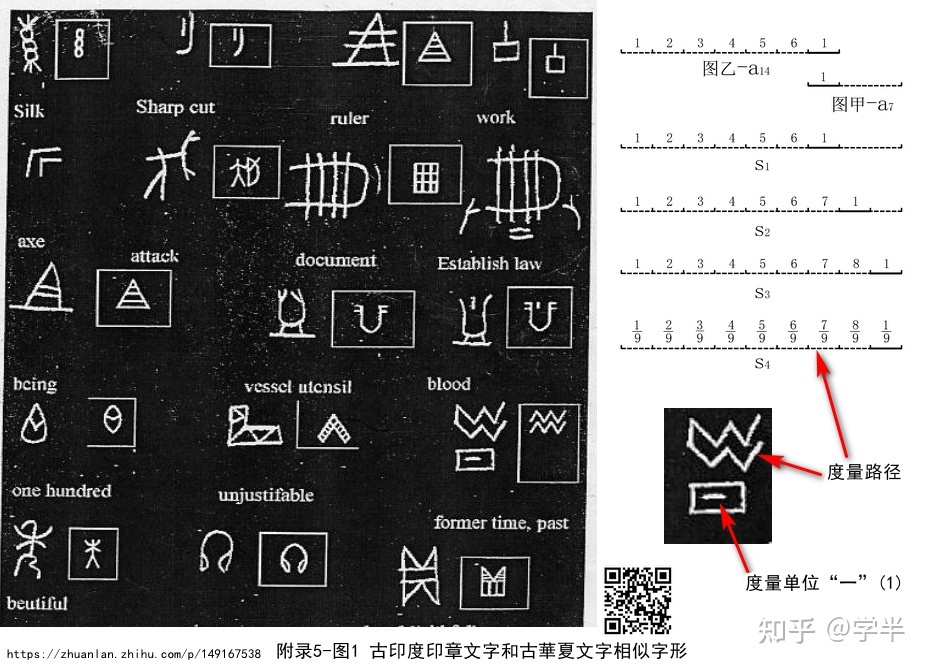
《易•說卦》中记载:“ ‘昔’者,聖人之作,《易》也。”《周礼•春宫•大卜》中记载:“掌三易之法:一曰连山,二曰归藏,三曰周易。”
这里说的“昔”者,即是指甲骨文“昔”字(图A)的字形所诠释的循环度量几何学模型,其为古代先贤圣人所掌“三易之法”中称为“周易”的一种,最早被以十进位制记数符号及其循环无限记数法明确记录在甲骨文中(图C),可以看作是远古文明时期的宇宙大一统数学科学历史的源头。
《普通高中教科书·物理必修 第一册》的序言说:“物理学:研究物质及其运动规律的科学”。
爱因斯坦说:“我们所说的物理学,包括这样一类的自然科学:它们的概念是以量度作为根据的;而且它们的概念和命题能够用数学形式来表示。因此,在我们全部知识中,那个能够用数学语言来表达的部分,就划为物理学的领域。随着科学的进步,物理学的领域扩张到拥有各个分科的程度,它似乎只受这种方法本身的界限所限制。……另一方面,从一开始就一直存在着这样的企图,即要寻找一个关于所有这些学科的统一的理论基础,它由最少数的概念和基本关系所组成,从它那里,可用逻辑方法推导出各个分科的一切概念和一切关系。这就是我们所以要探求整个物理学的基础的用意所在。认为这个终极目标是可以达到的,这样一个深挚的信念,是经常鼓舞着研究者的强烈热情的主要源泉。”
中科院物理所的曹则贤教授在《“新年悟理”2021跨年科学演讲:什么是相对论?》中说:“物理学主角就三个东西,时间、空间、物质,当然最后都是落到物质上。物质本身的存在让我们有位置或者有空间的感觉,而位置的变化就是运动,让我们有时间的感觉。”他还说:“1,2,3,4,5,6 这些数是有几何的,即‘数’的几何。……请大家记住,物理学是几何学!”
爱因斯坦在1936年发表的《物理学和实在》一文中指出:“我们的感觉经验,更概括地说,我们的一切经验都有一个重要性质,那就是它们的时间次序。这种次序导致主观时间这种心理概念,把我们的经验排成一个有秩序的纲目。然后主观时间通过有形物体概念和空间概念导致客观时间概念,就如我们以后会看到的那样。可是在客观时间观念之前,先有空间概念;而在空间概念之前,我们又发现有形物体的概念。后者是直接同感觉经验的复合相联系的。我们已经指出,作为‘有形物体’观念的特征的是这样一种性质:它使我们把观念同一种存在对应起来。”事实上,正是我们分辨出有形物体的“状态的改变”或“位置的变化”。这些运动形式让我们有(主观的)时间的感觉,也正是这种(主观的)时间观念表明了我们的感官所知觉到的运动者存在。
运动是物质的存在形式,几何上为了刻画物质的运动,必须有一个不动者作为参照。就是说,物质的存在性以动与不动的几何学形式相对性关系来辩证地描述:能够运动的是物质,没有物质就没有运动,则不动者只能是空无一物而称为空间。譬如将容器中所有之物移除,则该容器中为空,空者不能动。这就从有形物体的运动形式引入了绝对不动的虚空(假借有形物体虚构的几何空间)的概念,作为宇宙所有物质运动的虚构场所和容身处所。接着刻画物质在虚空中运动所经历的步程,就有了时间的概念。换言之,在几何学中,时间的概念无非是刻画宇宙所有的物质构成一个整体而同步在虚空路线上运动的过程——绝对运动的过程,就如我们以后会看到的那样。严格讲,物理学本质上是物质的几何学。
物理学的理论界都知道,爱因斯坦和玻尔为首的两大物理学派之间的争论主要在于两点:定域性和实在性原理。即定域性因果原理规定“任何物理效应都不可能以大于光速的速度传递”,客观现实存在性原理为保证“无论被观察与否都同样存在着一个现实”而引入一个隐变量(隐变量就是未被知晓的物理量的统称)。
哥本哈根学派的波恩和海森堡在1927年第五次索尔会议报告中说:“我们主张,量子力学是一种完备的理论,它的基本物理假说和数学假设是不能进一步修改的。”对此,十多年后爱因斯坦在1939年8月9日写给薛定谔的信中还说:“我仍旧确认物质的波动表示是实在状态的一种不完备的表示,尽管实际上已证明它本身是多么有用。揭示这一点的最妙的办法就是你所提出的关于猫(同‘杀猫’装置结合在一起的放射性衰变)的考查。……我仍旧认为,这种最值得注意的情况之所以会发生,是由于我们还没有得到一种关于实在状态的完备的描述。这种观点已经使我陷入十分孤立。我已经把它带到一种可以说是真正数学理论的地步,不过对它的检验自然是很困难的。”
但几乎所有的物理学家们都忽视了一个体系性的问题,即1935年爱因斯坦等人发表的“EPR论文”提要中说:“在一种完备的理论中,对于每一个实在的元素都该有一个对应的元素。使一个物理量成为实在的,它的充足条件是:要是体系不受干扰,就有可能对它作出确定的预测。” 在量子力学里,这个不受干扰的体系是也只能够是整个现实宇宙,否则体系就至少会受到量子干扰,因为量子是构成整个宇宙内部物质相互作用的最小微量成分或最基本单元。所以,定域性和实在性的定义必须修改为:
定域性——任何物理效应都不可能超出宇宙;
实在性——无论被观测与否都同样存在着一个现实宇宙。
这就发现或得到了一个理论初始假设或公理:“宇宙只有一个”,作为建立宇宙定域完备量子理论的统一基础或唯一出发点。若此,整个宇宙就是一个明确的定域显变量,任何物理效应都不可能超出宇宙;而且无论被观测与否都同样存在着一个现实宇宙,并不需要其它的隐变量。宇宙是一个完备而绝对孤立的物质系统,运动是整个宇宙的存在形式。
四、宇宙内部的相对性运动
关于宇宙内部的相对性运动,我们以整个宇宙(图1-a₁)为实验对象,即对图1-a₁施以一定形式的对折自我量度(运动),则得相对运动态的图1-a₂。经验地绳直图1-a₂,则得标量态的图1-a₃。将该标量态的图1-a₃,变换成矢量态的图1-a₄,是可能的。
运动是整个宇宙的存在形式。表整个物质宇宙的图1-a₄绕自身中心平旋两个直角,则得图1-a₅;图1-a₅绕自身中心平旋两个直角,则得图1-a₄;这种无休止而永恒的整体自旋,即整个物质宇宙于虚空中的运动(绝对运动),但这整个过程却具有形、数结合左右内向的对称(图1-a₆)。因为,宇宙整体自旋之绝对运动总是否定图1-a₄和图1-a₅的定量形式,而具有图1-a₆的定量形式表现。
在上述的逻辑推导过程中有以下几点值得注意:
对照形式逻辑同一律的公式“A是A”或“A等于A”,试问:上述的图1-a₃左侧的1/2是右侧的1/2吗?显然不是。换言之,在图1-a₃这里,如果用同一律的公式“A是A”代替“A等于A”则不真或不成立,也就是就会犯“偷换概念”或“偷换论题”的错误。其实,在用图甲来定量描述动者与不动者关系(图甲-a₃)的思维过程中,如果遵守同一律的公式而用“A是A”代替“A等于A”,同样会犯偷换“动者”(物质)与“不动者”(虚空)的错误,于是导致随后的思维过程不真。
在图1-a₃的基础上,根据形式逻辑的矛盾律,既不能判定图1-a₄右侧的1/2量大于左侧的1/2量成立(即否定图1-a₄右侧的定量形式),也不能判定图1-a₅左侧的1/2量大于右侧的1/2量成立(即否定图1-a₅左侧的定量形式)。从而只能判定图1-a₆的定量形式成立或为真。因为根据形式逻辑的排中律,上述矢量态的定量形式中必有一真,以消除矢量态定量的不确定性。
显然,图1-a₆这个真者包含作用和反作用矛盾着的互相抵触的两部分而总量为1/2+1/2=1(同一律:在同一个思维过程——定量刻画一个物质系统的各种运动的思维过程中,物质系统概念必须具有初始假设的图1-a₁确定的同一物质内容,以保持其定量思维的确定性,即图1-a₆=图1-a₁,亦即1/2+1/2=1,或图1-a₆是图1-a₁的运动形式表现),不妨将图1形式的上述逻辑规律称为(或定义为)“对立统一规律”。
正如列宁《哲学笔记》中说:“统一物[即图1-a₁,宇宙统一于物质]之分为两部分[图1-a₃]以及对它的矛盾[图1-a₆]着的部分[图1-a₆的右侧或左侧的物质最小微量及其动向变换]的认识,是辩证法的实质(是辩证法的‘本质’之一,是它的主要特点或特征之一,甚至是它的最主要特点或特征)。”
事实上,先秦时期中国的先贤已经发现,真正数学理论中几何图形度量(运动)的叠合法必须建立在物质实践感官经验的(感性认识的)物有形、再为形配数所得的形数统一或相结合几何学形式明确定量表述的公理:“宇宙只有一个”的基础上(图甲),或者欧几里得几何学的叠合法必须用可具体操作的物质量杆对折自我量度(运动)这种探讨全等的方法(图1)来代替。
前述图甲和图1中的经验事实表明,可先给出现实存在的实物线段,再定义线上的点,点为线之界,界之间为形。根据形式逻辑的同一律,线有形可分而分之不竭者(称为“量子”或“物之精也”)仍为线,而不可为点或点的集合。即《庄子·秋水》中说:“夫精[细微小]粗[大]者,期[度量求解]于有形者也。无形者,数之所不能分也。不可围[即无界]者,数之所不能穷也。可以言论者,物之粗[大者]也。可以意致[推理求解]者,物之精也。”若此则不难设想,中国古代学者按照形数结合几何学形式严格直观的“一尺之捶[实物线段,作为整个宇宙的几何直观抽象,即图甲-a₅中的实者,亦即图1-a₁或图1-a₆],日取其半[以线段对折的自我量度方式定义线段中分点而取损其半,损之又损之],万世不竭”这种几何物理方法,可精确求解得宇宙物质一次又一次地不断分割下去最终的无穷小微量——量子。详述之则为:
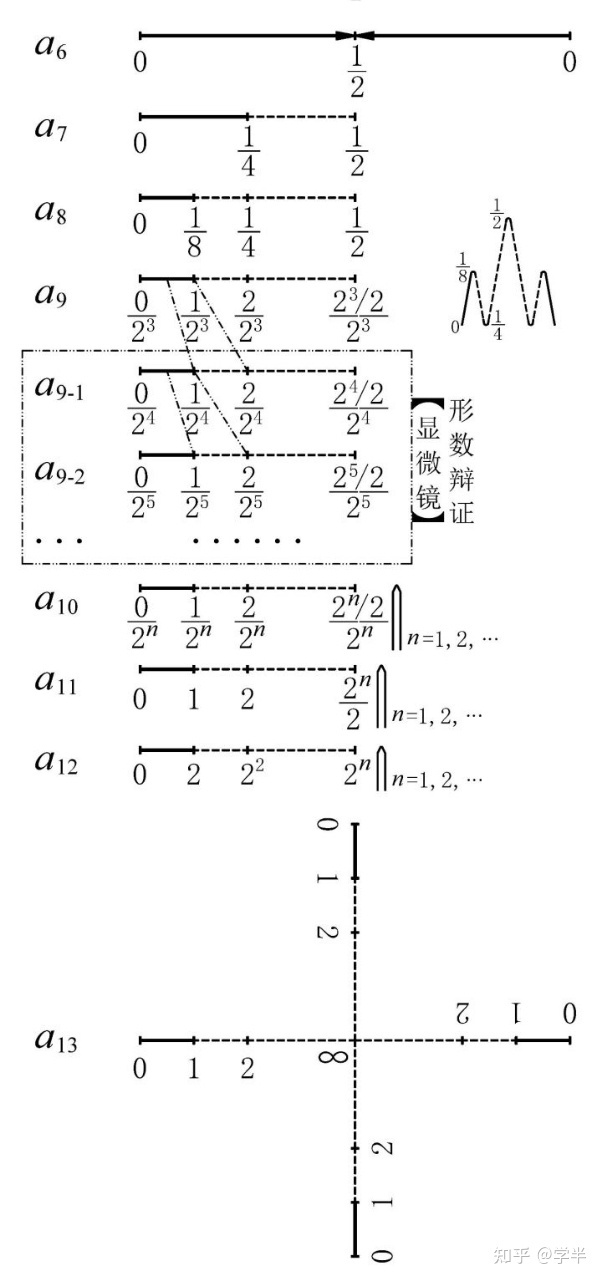
运动是物质宇宙的存在方式。表整个物质宇宙的图2-a₆(即图1-a₆)内部的相对性运动只能够首先是内耗的排斥,其几何形式表现只能够首先是形、数结合的几何分形及其张量态。即:
(1)几何分形。对图2-a₆施以实取损[或耗损]其半,则得图2-a₇;接着对图2-a₇实取损其半,则得图2-a₈;对图2-a₈施以通分,则得图2-a₉;将图2-a₉一般化,则得图2-a₁₀。
(2)几何分形的张量态。对图2-a₁₀施以几何物理方法(俗称“数学物理方法”)的张量运算,即将图2-a₁₀扩大2ⁿ倍,则得图2-a₁₁,以描述宇宙的暴胀;接着将图2-a₁₁扩大2倍(2是张量的最小整数),则得图2-a₁₂,以描述宇宙的膨胀,其张之入微而不可再张,即宇宙内部物质混沌运动的暴胀和膨胀过程无为而终。将图2-a₁₂展开,则得平面态的图2-a₁₃。
在图2-a₁₂及其展开的图2-a₁₃中,量子就是构成整个宇宙物质系统的几何最小微量成分或最基本单元,与图2-a₁₂及其展开的图2-a₁₃中的实者大小相等,古称“则”,即“等画物也”(《说文解字》:“则,等画物也”)。《淮南子·诠言训》:“夫无为,‘则’得于一也,一也者,万物之本也[度量宇宙物质的最基本单元],无敌之道也”。《庄子·缮性》:“道,理也”;《说文解字 · 一》:“一,惟初大极[惟初即理性思惟初始,大极者宇宙也],道立于一[宇宙几何学理论建立在公理‘宇宙只有一个’的基础上]”。
几何直观表明,物质的量子是用形数结合几何学形式的量子数(图2-a₁₂及其展开的图2-a₁₃,又称“物质的自然数”)来刻画或表征的,量子数可以是整数(图2-a₁₂中的数)或半整数——图2-a₁₃中的数。这种完备的宇宙自然数或物质量子数为真,而且与皮亚诺公理所定义的自然数不一致。
其实,图2-a₁₃的几何直观表明,依据宇宙几何学公理推导出来的一个无穷(∞)命题是一致位居宇宙中央的几何连续统基数。但是按照欧几里得几何公理构造或推导得出的笛卡儿直角坐标系的数轴上的两个无穷(-∞、∞)命题是直观不一致的。而且,所有的数都作为量子几何单元之界,界之间为量子的形,形是数之根。
恩格斯《自然辩证法》中说:“我们所面对着的整个自然界[图2-a₁₂及其展开的图2-a₁₃]形成一个体系,即各种物体相互联系的总体,而我们在这里所说的物体,是指所有的物质存在,……这些物体是互相联系的,这就是说它们是相互作用着的,并且正是这种相互作用构成了运动。”又:“数学——辩证的辅助工具和表现形式。”
五、量子纠缠现象的理论描述
上述描述物质相互作用的量子数系统,可以完整解释物质系统从整个宏观宇宙到微观量子过程所有的可观测量的演化行为,从而避免掉任何不确定性或概率性。
以对量子纠缠现象的理解为例,在量子力学中,描述物质实在状态的波函数ψ的表达形式——代表“死”的那部分波函数同代表“活”的那部分波函数等值地混合在一起。爱因斯坦坚持认为物质实在状态的波动函数表示是不完备的。详情可参见《爱因斯坦文集》第一卷382页,该页为1939年8月9日爱因斯坦给薛定谔的信,其中谈到薛定谔关于猫(同‘杀猫’装置结合在一起的放射性衰变)的考查。薛定谔用一个“杀猫”的理想实验揭示波函数ψ的不完备性,意思是讽刺玻尔派的波函数所提供的对客观实在状态的描述,就像可观察到死和生(活)状态同时叠加在一起的猫;但现实中像这种猫一样的物质物理过程是不存在的,因为物理学中任何状态的转变都是描述一个过程:运动。其实,只要把上述波函数ψ中的“死”、“活”两部分内容分开为ψ1(描述“死”的状态)以及ψ2(描述“活”的状态),用严格直观的几何形式(防止实数理论以及微积分运算偷换点与线的概念)来描述就清楚了,如:ψ1=图2-a₁₂=图3-a₁ (死);ψ2=图3-a₂ (活)。
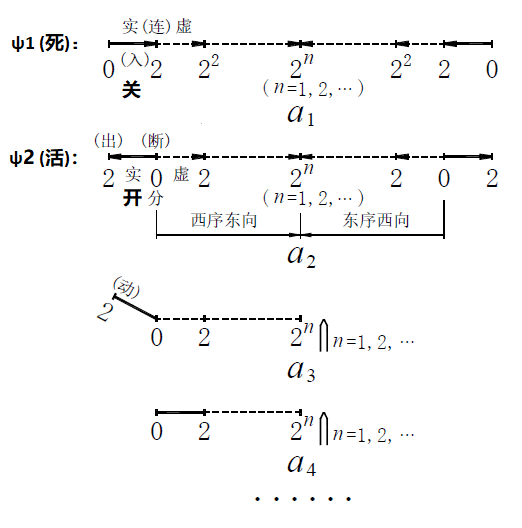
在描述宇宙系统内部物质运动的图3中:
虚线(┅┅┅)或实线(━━━)皆为物质的形,形数结合(形以数为界定量)则构成矢量(向量),可表明量子物质聚散(吸引或排斥)相互作用及其动向变换。
一个自旋角动量为零的物质系统(ψ1,即图3-a₁)排斥和发出的两个光子分别对应于ψ2(即图3-a₂)中左侧的实线段“2━0”和右侧的实线段“0━2”(称为“实量子”,左、右两者自旋方向相反),其通过ψ2中的虚线段“0┅2┅┅2ⁿ┅┅2┅0”(称为“虚量子”构成的量子场)连结成一个整体。ψ2(即图3-a₂)处于离散的排斥过程终结而转变为凝聚的吸引过程开始的状态。整个体系内部量子物质之间的作用与反作用大小相等方向相反。
整个体系不受外部干扰(参“EPR论文”提要[12]),一切观测设备和环境因素都包含在体系中。观测信号可以看作虚量子“0┅2”。一旦ψ2(即图3-a₂) 中的实量子“2━0” 绕“0”动转迭合到虚量子上(见图3-a₃及图3-a₄,称为“量子迭代”),即表示实量子被观测到(此时实量子矢量的指向发生转变并与虚量子的指向一致)。根据系统角动量守恒,可预言左侧和右侧的量子迭代一定同时发生(即具有对称性),这就是所谓的“瞬时(同时)作用”。所以,实验观测到纠缠量子对的瞬时(同时)作用这一事实,无非是整个系统角动量守恒的证据。这就证明了爱因斯坦主张的光速定域性原理不成立。
事实上,中国古代的先贤已经解决量子“死、生”状态纠缠不清的问题。换言之,量子“死、生”状态怎样严格区分确定的问题,是作为物质运动的过程来描述的;任一物质过程终结(死),则有下一相邻过程开始(生)。即《庄子·知北游》:“生也死之徒,死也生之始,孰知其纪![譬如]人之生,气之聚[量子吸引凝聚]也。聚则为生[量子引力发生,即ψ2],散则为死[量子排斥过程终结,即ψ1,亦即图2-a₁₂或图2-a₁₃]。若死[即ψ1],生为徒[即ψ2],吾又何患!故万物一也[宇宙统一于物质]。”在这里,死、生状态转变用量子宇宙(图2-a₁₂或ψ1)的局域等值变换或几何整数微分(ψ2)来描述,ψ1表征宇宙物质量子化耗散的排斥过程终结(死);ψ2表征量子之间凝聚的吸引相互作用出现,从而量子凝聚形式宇宙过程开始(生)。因为量子凝聚形式宇宙过程用几何整数无穷积分(集合)的量子迭合代替运算(即图3-a₂、图2-a₃及图3-a₄,简称“迭代”)来描述,所以ψ2是其迭代过程的初始条件或边界条件。
六、七、八节请移步详参以下链接
https://zhuanlan.zhihu.com/p/619697794

九、结语
华罗庚《数学的用场与发展》:“对宇宙的认识还将有多么大的进展,我不知道,但可以说,每一步都是离不开数学这个工具的。”华罗庚猜想道:“是否有一个统一的处理方法,把宏观世界和微观世界统一在一个理论之中,把四种作用力统一在一个理论之中,这是物理学家当前的重大问题之一。不管将来他们怎样解决这个问题,但是在处理这些问题的数学方法必须统一。必须有一套既可以解释宏观世界又可以解释微观世界的数学工具。数学一定和物理学刚开始的时候一样,是物理学的助手和工具。在这样的大问题的解决过程中,也可能同牛顿同时发展天体力学和发明微积分那样促进数学的新分支的创造和形成。” 可以说,上述的华罗庚猜想,是数学历史上最伟大的科学猜想。
大家都知道,数学的基础是数论。但是,当今几乎没有人知道,数论的根基是整数的几何理论,其整数首先是以实物的形、数统一或相结合几何学形式(纯数学形式)开始定量刻画整个物质宇宙的数“一”(图甲–a₅,绝对动的一之形表整个宇宙)。事实上,中国古代的学者提出了公理“宇宙只有一个”,作为宇宙几何学形式理论演绎体系的统一基础或唯一出发点,从此开创了一门宇宙几何学形式的数论学科,以定量刻画整个宇宙的各种运动和规律。若此,将促进实事求是的纯理论数学守正创新,引领未来世界科学理论发展新方向。
附录
证明论有关词条解释(来源:《辞海》微信版)





全部评论(1)